INED researcher Carlo-Giovanni Camarda and Ugofilippo Basellini of the Max Planck Institute for Demographic Research (MPIDR)

The Lee-Carter model takes into account ages and given year or period to determine overall mortality rates for an entire population. It’s a fundamental model, but it cannot be used to examine life expectancy fluctuations and trends according to chosen criteria; that is, by demographic components and as a function of trends in those components over time. The Lee-Carter model is based on the assumption that specific improvements by age are linear across a given period and projections are constructed using that same principle. 

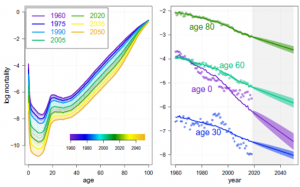
We were interested in producing more accurate mortality forecasts. To do so we developed a three-component Lee-Carter model (3C-sLC) that uses the initial Lee-Carter model while making it possible to divide the study of mortality into three subcategories: children, adults, and older persons. In this way researchers can analyze mortality by subgroups and so break it down. They can also get a better understanding of interdependencies between different ages, which in turn allows them to intervene in projections. 

Our 3C-sLC model makes it possible to obtain less rigid or fixed mortality projections. This means the projections are less certain, but it also means they reflect reality more accurately because they take account of more parameters. We used this approach on data on ten groups with low mortality. The new model works particularly well for studying male mortality because excess mortality among young men is clearer. But to analyze female mortality, all that is needed is a two-component variation on the 3C-sLC model (child mortality and mortality in old age). 

Our aim with this model is to provide actuaries, demographers, epidemiologists and social science researchers generally with a unique, precious tool that will simultaneously smooth, break down, and predict mortality figures.